机器学习（一）：线性回归（Linear Reggression）

发表于 | 分类于 | 0 comments

线性回归 Linear Reggression

线性回归是一种回归算法，是一种基础的机器学习算法。

  • 回归问题解决的是对非离散值的预测，例如房价预测、股价预测等。线性回归是解决这类问题最基础的算法，也是神经网络等算法的基础。
  • 分类问题解决如图片分类、文本分类等问题，分类问题包括二分类、多分类等。逻辑回归尽管名字有回归二字，其实是一种分类算法。

拿$(\theta_0,\theta_1)$这样两个参数的线性表达式为例， $h = \theta_0 + \theta_1x$，h为预测值（例如房价），x为训练数据的特征值（例如房子面积），𝛉i为参数。所谓线性回归，即输入训练数据的一组特征值，得到预测值h，h与x成线性关系，推广到多维矩阵，表达式如下：

$h_\theta(x) = \theta^TX = \theta_0x_0 + \theta_1x_1 + \theta_2x_2 + … + \theta_nx_n$

根据预测值与实际值的误差来调整参数$\theta$，可以使h与实际值具备更好的拟合效果。通常我们用损失函数(loss function)或代价函数(cost function)来衡量当前模型h与实际值的拟合效果。 例如预测值为8.0，实际值为10.0，由此得误差为2，累加计算均方误差，推广到多个特征的表达式如下：

$J(\theta_0, \theta_1…\theta_n) = \frac{1}{2m}\sum_{=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2 $

其中h为预测值，y为实际值。 基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。

得到损失函数后，要使模型的效果得以提升，需要调整参数$\theta$，使得均方误差最小，一般有两种方法。

  1. Normal equation
    直接对该损失函数求解最小值，即对𝛉求导，使导数为0。通常我们用矩阵的形式来表达，推导过程如下(此处用’表示矩阵转置)：

X为输入特征值矩阵，N为X的维度，y为实际值组成的向量，𝛉为所求参数矩阵。
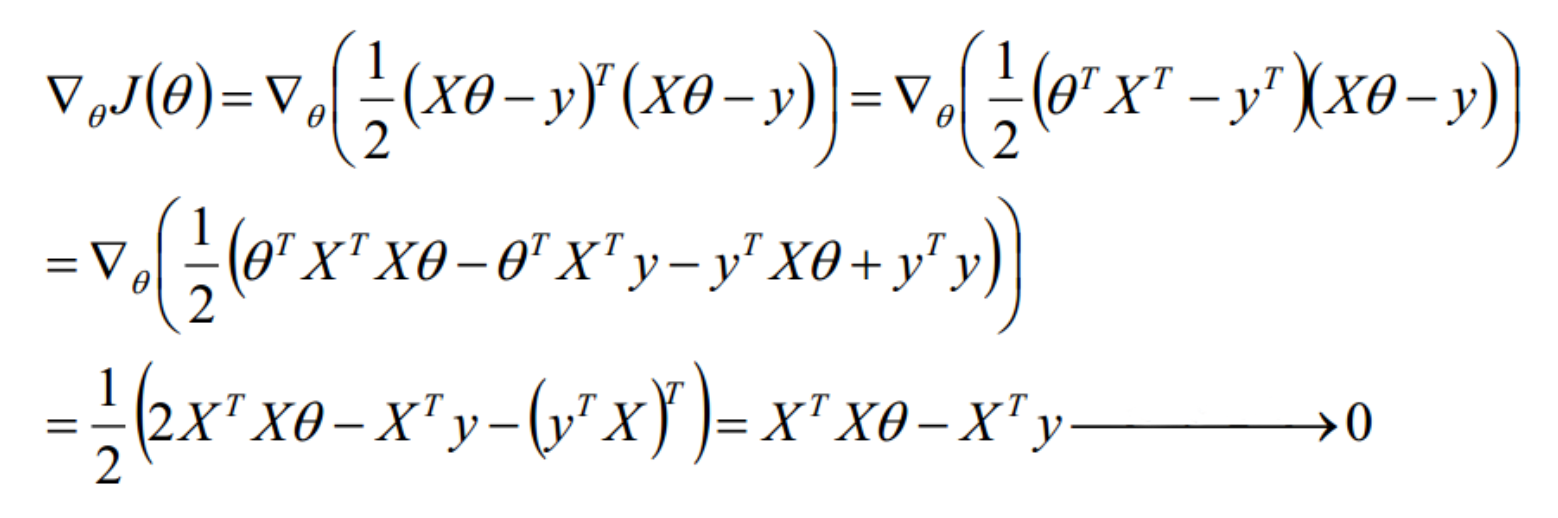得𝛉值为：$\theta = (X^TX)^{-1}X^Ty$

​

可使用正则化避免X‘X不可逆与模型过拟合。即在X’X项上加上lambda*I（I为单位矩阵）。

由于矩阵求逆一般在O(n^3)这个复杂度的量级上，随着数据量的增大将花费大量的时间，因此在数据量较大的情况下，不使用Normal Equation这个方法。

​

  1. Gradient Descent 梯度下降

梯度下降通过学习率$\alpha$迭代更新$\theta$，具备良好的性能与实现效果。
在梯度下降中，$\theta_j$通过每次减去损失函数对自身求偏导数的值与$\alpha$的乘积来更新自身。有下图可知，当偏导数大于0时，$\theta_j$减小，在坐标轴上左移；当偏导数小于0时，$\theta_j$增大，在坐标轴上右移动。每次$\theta_j$值的变化总是在去接近损失函数的最小值。

梯度下降表达式为：$\theta_j = \theta_j - \alpha\frac{\partial{J}(\theta)}{\partial\theta_j}$

线性回归Tensorflow简单实现梯度下降

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
​	
# 生成测试数据，𝛉1为0.1, 𝛉0为0.2
points_num = 100
vectors = []
​	
for i in range(points_num):
    x1 = np.random.normal(0, 0.66)
    y1 = 0.1 * x1 + 0.2 + np.random.normal(0.0, 0.02)
    vectors.append([x1, y1])

x_data = [v[0] for v in vectors]
y_data = [v[1] for v in vectors]
​	
# 绘制测试数据
plt.plot(x_data, y_data, 'ro', label='Original data')
plt.title('LR using GD')
plt.legend()
plt.show()
​	
# Tensorflow实现
W = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
b = tf.Variable(tf.zeros([1]))
y = W * x_data + b
loss = tf.reduce_mean(tf.square(y - y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.mi÷nimize(loss)
init = tf.global_variables_initializer()
​	
with tf.Session() as sess:
    sess.run(init)
    for step in range(40):
        sess.run(train)
        print('Step={0}, Loss={1}, [Weight={2}, Bias={3}]'.format(step, sess.run(loss), sess.run(W), sess.run(b)))
    plt.plot(x_data, y_data, 'rx', label='Original Data')
    plt.title('LR using GD')
    plt.plot(x_data, sess.run(W) * x_data + sess.run(b), label='Fitted Line')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()

拟合效果如下：