33. 丑数
把只包含因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
思路:常规暴力解法很容易想到,即计算每一个数是否为丑数,若是丑数则计数加一,算到第n个丑数,返回。但是这种解法效率不高,因为对于每一个数字都要计算,相当冗余。
实际上,丑数一定是由小于它的另一个丑数乘以2,3,5得来,那么对于第n个丑数k,它可能是由k/2,k/3,k/5得来的。
反过来正着想,第一个丑数为1,第二个丑数一定是1*2,1*3,1*5中较小的那个,由此得到第二个丑数为2;第三个丑数一定不会再由1*2得到,且一定大于1*2,因此我们比较2*2,1*3,1*5中的最小者……如此循环,计算n次返回。
例,设定m2,m3,m5三个计数器
| i | m2 | m3 | m5 | uglyNum |
|---|---|---|---|---|
| 2 | 1*2 | 1*3 | 1*5 | 2 |
| 3 | 2*2 | 1*3 | 1*5 | 3 |
| 4 | 2*2 | 2*3 | 1*5 | 4 |
| 5 | 3*2 | 2*3 | 1*5 | 5 |
| 6 | 3*2 | 2*3 | 2*5 | 6 |
| 7 | 4*2 | 3*3 | 2*5 | 8 |
注意,在i=6时候,我们得到丑数为6,下一个循环应该将m2和m3都往后推一个,因为我们之前得到的6可以由丑数3*2得到,也可以由丑数2*3得到,因此需要将这两个计数器各自加一,否则下一轮计算中,会再次得到上一轮计算过的丑数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
public int GetUglyNumber_Solution(int index) {
if(index == 0) return 0;
int[] ugly = new int[index];
int m2 = 0, m3 = 0, m5 = 0;
ugly[0] = 1;
for(int i = 1; i < index; i++){
ugly[i] = Math.min(ugly[m2]*2, Math.min(ugly[m3]*3, ugly[m5]*5));
if(ugly[i]%2==0) m2++;
if(ugly[i]%3==0) m3++;
if(ugly[i]%5==0) m5++;
}
return ugly[index - 1];
}
}
34. 第一个只出现一次的字符
在一个字符串(1<=字符串长度<=10000,全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置
思路: 统计字符出现次数,如果为1,则返回字符串中第一个为1的字符的下标即可。统计字符可以使用java的HashMap,遍历一遍整个字符串。遍历完成之后,再遍历一次字符串,若字符在HashMap中存储的次数为1,则返回。因为字符串为顺序遍历,因此第一个次数为1的字符一定就正解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import java.util.HashMap;
public class Solution {
public int FirstNotRepeatingChar(String str) {
if(str.length() == 0) return -1;
HashMap<Character, Integer> w = new HashMap<Character, Integer>();
char[] strlist = str.toCharArray();
for(int i = 0; i < strlist.length; i++){
if(!w.containsKey(strlist[i])) w.put(strlist[i], 1);
else w.put(strlist[i], w.get(strlist[i]) + 1);
}
for(int i = 0; i < strlist.length; i++){
if(w.get(strlist[i]) == 1){
return str.indexOf(strlist[i]);
}
}
return 0;
}
}
35. 数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
输入描述:
题目保证输入的数组中没有的相同的数字数据范围: 对于%50的数据,size<=10^4 对于%75的数据,size<=10^5 对于%100的数据,size<=2*10^5示例1
输入
1,2,3,4,5,6,7,0输出
7
思路: 挺坑的一道题,代码略长,递归写的不熟练,出现了一些边界上的问题,去IDE里debug了一下才解决。按常规思路,暴力求解一定能求,复杂度$O(n^2)$,但是这题显然涉及到大数运算,这样求解必然超时。因为逆序对实际上是两个两个比较,一开始是从相邻的两个数开始比较,且逆序数满足i < j,nums[i] > nums[j],可以想到,归并排序是非常符合这个条件的,因为归并排序到base case的时候就是相邻的两个数在比较,且左侧的下标都小于右侧,只要左侧的数大于右侧,即成为一个逆序对。因此,使用归并排序将数组降序排列就能得到问题的解,复杂度为$O(nlogn)$。
例,
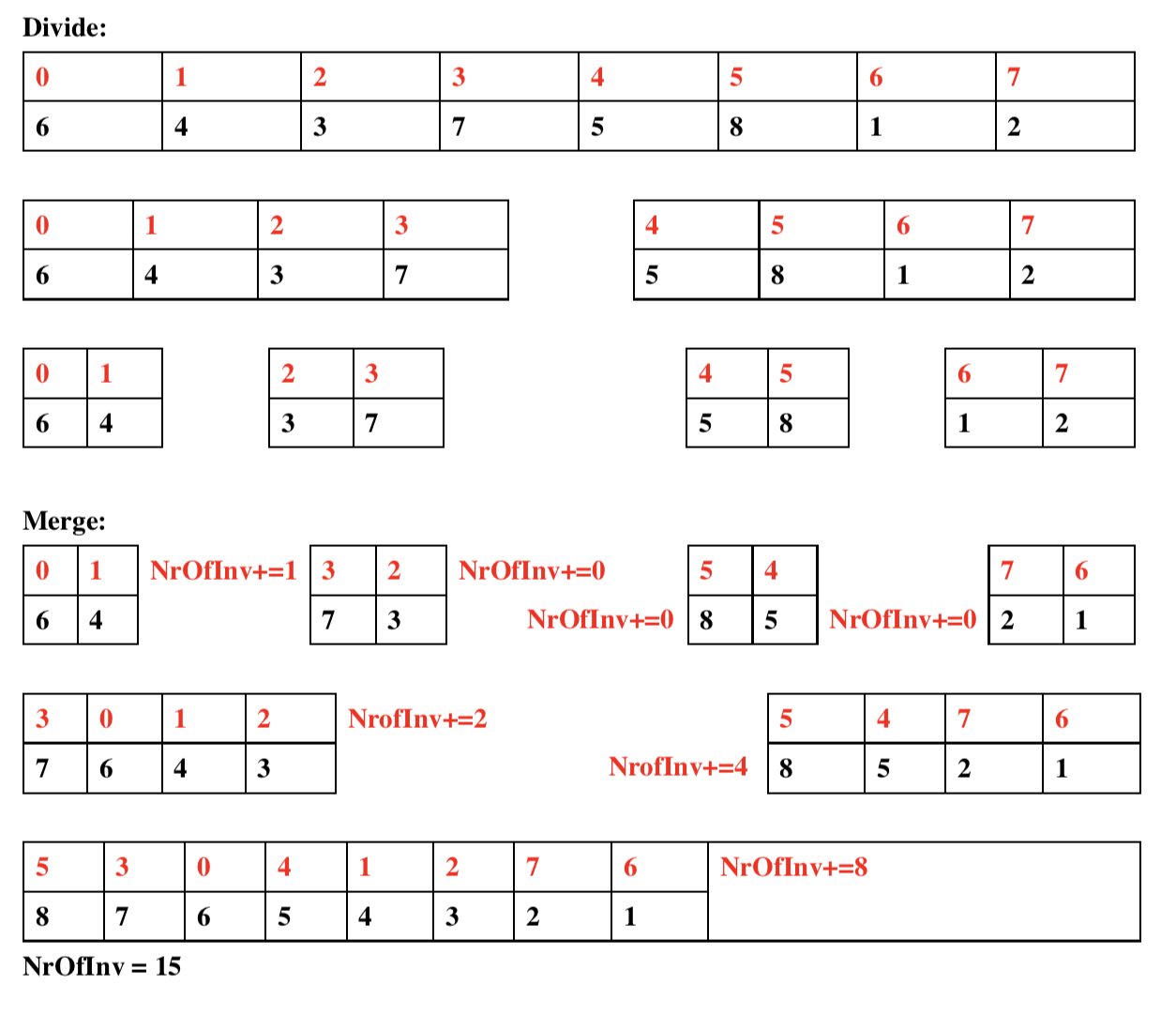
但是这里要注意的是,测试用例的数字非常大,在代码中必须使用long类型计数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public class Solution {
public int InversePairs(int [] array) {
long count = 0;
count = sort(array, 0, array.length - 1);
long res = count%1000000007;
return (int)res;
}
public long sort(int[] array, int start, int end){
if(start == end) return 0;
int mid = (start + end) / 2;
long left = sort(array, start, mid);
long right = sort(array, mid+1, end);
return merge(array, start, mid, end) + left + right;
}
public long merge(int[] array, int start, int mid, int end){
long count = 0;
int k = 0;
int l = start, r = mid + 1;
int[] tmp = new int[end - start + 1];
while(l <= mid && r <= end){
if(array[l] > array[r]){
count += (end - r) + 1;
tmp[k++] = array[l++];
}
else if(array[l] <= array[r]) tmp[k++] = array[r++];
}
if(l > mid){
for(int i = r; i <= end; i++){
tmp[k++] = array[i];
}
}
else if(r > end){
for(int i = l; i <= mid; i++){
tmp[k++] = array[i];
}
}
for(int j = 0; j < tmp.length; j++){
array[j + start] = tmp[j];
}
return count;
}
}