字符串——后缀数组
学习资料:论文链接
名词概念
后缀 Suffix[i]表示从i到字符串末尾的一个子串,
字符串大小比较 指按字典顺序比较,对于两个字符串u、v,令i=1,比较u[i]和v[i] ,若相等则i+=1,若u[i] < v[i],则 u<v,反之亦然。如果 i > len(u) 或者 i > len(v) 仍比较不出结果,那么,若 len(u) < len(v) 则 u < v ,若 len(u) = len(v)则 u = v ,若
len(u) > len(v)则 u > v。由此可知字符串的任意两个后缀,因其长度不等,大小亦不相等。
后缀数组 一个字符串s,其长度为n,它的后缀数组SA是一个一维数组,该数组保存的是[1…n]的某个排列,该排列是后缀按大小升序排列后的i值,满足Suffix(SA[j]) < Suffix[SA[j+1]]
例:s = ‘ aabbaca ‘
名次数组 Rank[i] 保存的是后缀按从小到大顺序排列后,Suffix[i]的名次。例:Rank[1] = 2,Rank[4] = 3
问题描述
给定文本T,其长度为n;查询样本为P,其长度为m。
如何利用后缀数组在T中快速查找P的位置?
利用性质:一个字符串的任何子串都可以看做是它某个后缀的一个前缀。
我们可以利用二分查找寻找到子串的位置。算法如下:
初始化 j = n/2
比较 T[ SA[j] : n-1 ] 和 P,此次比较需要至多 m次比较,若 T[ SA[j] : n-1 ] = P 则,返回SA[j];若 P < T[ SA[j] : n-1 ],则查找SA[j]之前的后缀;若 P > T[ SA[j] : n-1 ],则查找SA[j]之后的后缀。
例:在s = ‘ aabbaca ‘ 中查找 ‘ ab ‘

由ab是abbaca的前缀可知ab的位置为 SA[2] = 1。
其时间复杂度为O(mlogn)。
如何找出T中所有的P?
多个P的存在,说明在S的所有后缀中,有多个后缀具有相同的前缀。因为SA是按照后缀的字典顺序排序的,因此这些具有相同前缀P的后缀在SA中的位置是连续的。根据此性质,我们可以用两个二分查找去锁定SA中的这段连续范围。其时间复杂度为O(mlogn+k),k为P的数量。
例:在s = ‘ aabbaca ‘ 中查找子串 ‘ a ‘ 的出现次数
首先利用二分查找到做左边界,得 j=0,SA[j] = 6

同样使用二分查找,找到右边界,得 j=3,SA[3] = 4

SA[0] 到 SA[3] 共4个后缀的前缀为 ‘a’ ,得共出现4次。
如何构建后缀数组
倍增算法
利用新建rank数组用来存储后缀的排序。
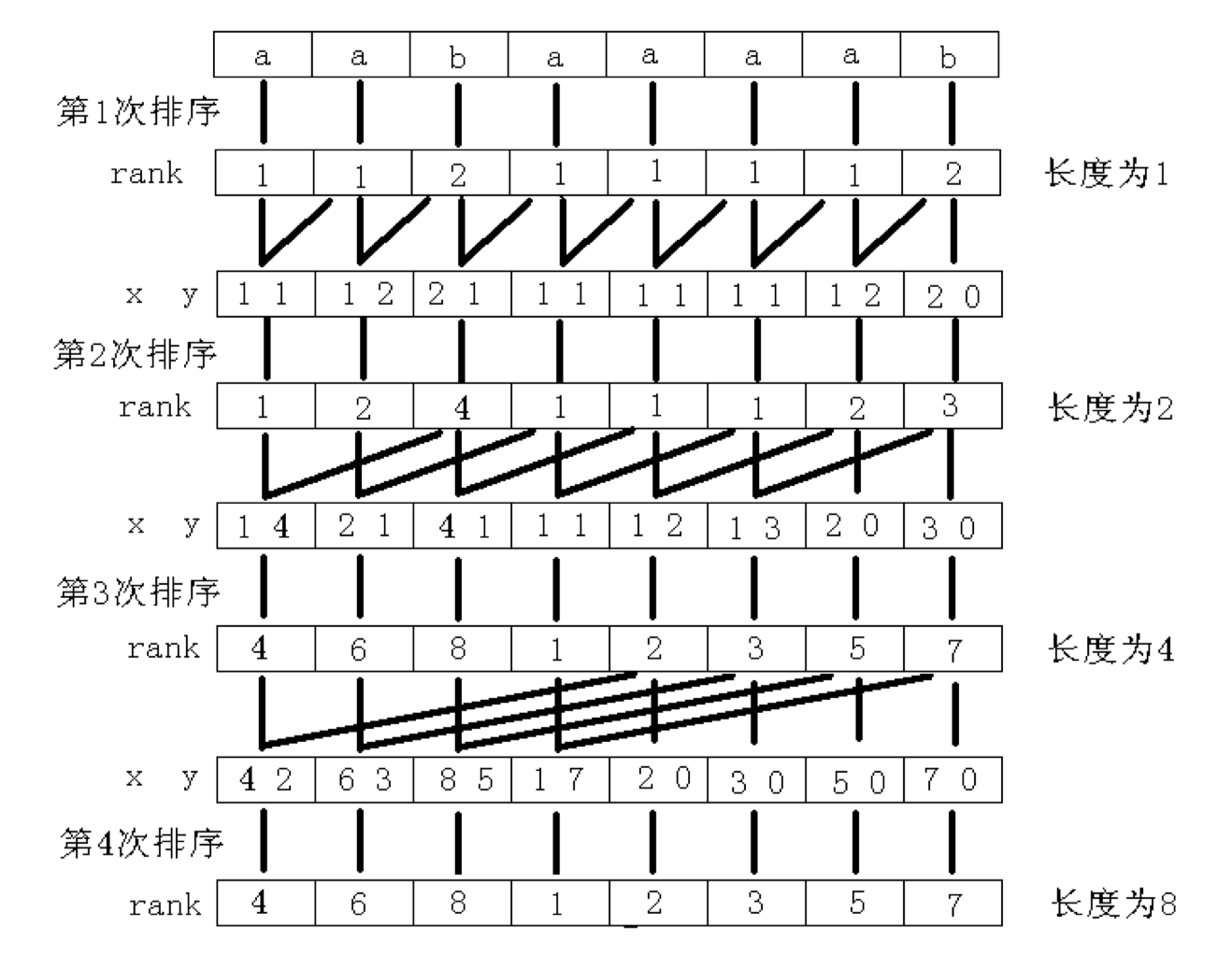
图片来自论文-论文链接
这张图其实很好的解释了最终rank是如何产生的。我们会发现后缀都是由一个较短的已知后缀和前半部分组成的。从图中我们可以看到,从第三次排序到第四次排序之间的组合,就已经把所有后缀的包括在内了,这里的排序采用基数排序,从之前获取的排序信息,可以很容易得到组合后的排序。
例,求 ‘abcaabccabcac’ 的后缀数组:
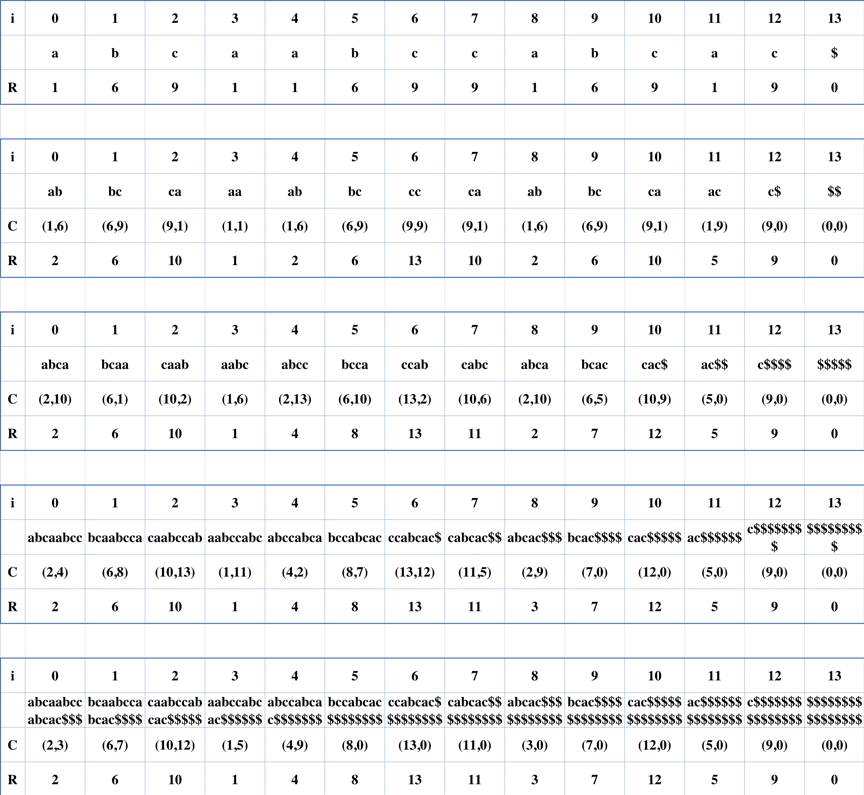
SA = [3, 0, 8, 4, 11, 1, 9, 5, 12, 2, 7,10, 6]